The Ideal Gas from first principles

We explore the connection between the microscopic world of particles and the macroscopic world of gases. This should be accessible to high school students with an interest in math and physics. Making some simple assumptions about how particles move and how gases behave, we derive the ideal gas law which connects pressure (P), volume (V) and temperature (T).

Let's imagine a box of volume V filled with N particles. One of its faces has an area A.

If that face was free to slide, the pressure from the gas could push it outwards, like so:

Instead, we imagine containing the gas, by providing the necessary pressure from the outside.

Pressure is simply the force per unit of area, $P = \frac{F}{A}$ . So our question is:

what force F do we need to exert to prevent the gas from expanding?

A single particle

Let's assume a particle collides with a face of the box in an interval of time Δt. Let's start by considering the force necessary to contain a single particle.

Let's assume this particle is moving with velocity v, which has 3 components, v_x along the x direction, v_y along y and v_z along z. Let's consider our moving wall is along the x direction, and ask about for force that this particle creates on it.

Assumption: The particle obeys Newton's laws

It will thus move according to Newton's 2^nd law:

F = \frac{\Delta p}{\Delta t}

Assumption: Collisions with the walls of the box are assumed to be elastic.

Note that elastic, in this context, means something different from the elasticity of a rubber band or a spring. An elastic collision is one in which momentum and kinetic energy are conserved. By contrast, in an inelastic collision, the kinetic energy before the collision can become sound, heat, or an internal vibration or deformation of the object.

Atoms are assumed to collide like perfect billiard balls (and produce no sound, since there is no air between them to carry any sound!).

Let's imagine what would happen if collisions between particles in the gas and particles in the wall were not elastic. Some particle would fly towards the wall with kinetic energy $KE=A$ , then come back with $KE=A' < A$ . So it would lose energy when it hits the wall. Since the overall energy is conserved, the particles in the wall must have gained some of that kinetic energy. After trillions and trillions of collisions, the average kinetic energy of the particles on the wall would increase. Thus the gas would cool and the wall would heat up.

To describe a perfectly elastic collision of a particle with the wall, in the x component we can write:

F_x = \frac{\Delta p_x}{\Delta t}= \frac{-mv_x - mv_x}{\Delta t}

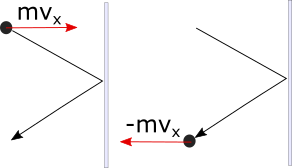
So in order to prevent one particle from pushing on the wall, the wall would have to exert a force of $\frac{-2mv_x}{\Delta t}$ , where the negative sign tells us it points to the left. But of course, a gas will have many particles hitting the wall.

A basketball will typically have 180,000,000,000,000,000,000,000 molecules inside it! That's a lot of potential collisions!

Our next question is, how many of those particles are hitting the wall? Let's call N the total number of particles in the box. Many will be towards the center of the box, or on the other side of it. We are interested in the face of the box labelled A. How many particles are hitting that wall in a time interval Δt? Let's call that number N_↦. This is the number of particles going to the right in the x direction that will be close enough to hit the wall in a time Δt.

Let's consider a volume V _↦, close to the wall of area A. The molecules moving to the right fast enough will hit the wall before a time Δt has elapsed.

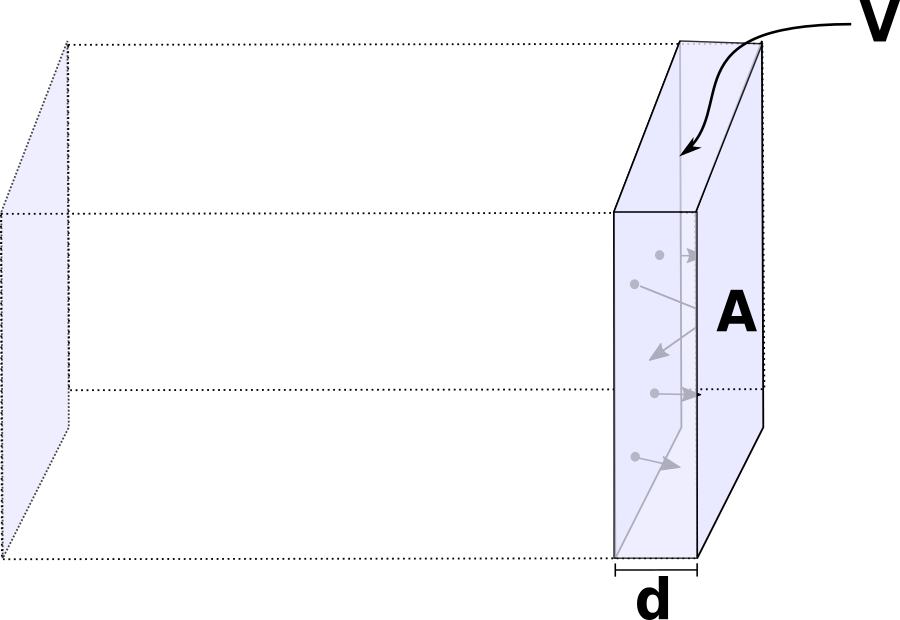
7.volume_that_will_hit.png

How can we quantify this volume and what does "fast enough" mean here?

The volume can be written as: V _↦ = d A. The length of the side times the area of the wall. If we want a molecule inside V _↦, moving to the right, to reach the wall in a time Δt, it will have to travel a distance d. In other words, if a particle inside V _↦ moves to the right with velocity v_x, it will cover a distance d = v_x Δt. The volume of the box which contains particles that will hit is thus V _↦ = v_x Δt A.

Now, to find the force that these particles exert on the wall, we need to know how many will hit the wall. If N_↦ are going to hit in a time $\Delta t$ , they will, together, exert a force:

F_x = N_{\mapsto} \times \frac{-2mv_x}{\Delta t}

The total force will be the sum of the force exerted by each one of the N_↦ particles hitting the wall. So how many particles hit the wall? If V is the total volume of the box, and N the total number of particles, the particles hitting the wall will be:

$N_{\mapsto} = \frac{1}{2} N \frac{V_{\mapsto}}{V}$

the 1/2 factor comes because, on average, half the particles in V_↦ are going to the right and half are going to the left. The other factor is the volume containing particles that will reach the wall, over the total volume. Let's imagine only a sliver 1/100 of the volume contains particles close enough to hit the wall after a time Δt. Then N/200 would be the particles hitting the wall.

Coming back to the total force exerted on the surface A, we can rewrite it as:

F_x = \frac{1}{2} N \frac{V_{\mapsto}}{V} \left( \frac{-2mv_x}{\Delta t} \right) \label{ref4}

Replacing, V _↦ = v_x Δt A into ( $\ref{ref4}$ ) we obtain:

$F_x = \frac{1}{2} N \frac{v_x \Delta t A}{V} \left( \frac{-2mv_x}{\Delta t} \right)$ . However, note that $\Delta t$ and the number 2 are in the numerator and the denominator. We can thus simplify to: $F_x = \frac{1}{\cancel{2}} \frac{N}{V} v_x \cancel{\Delta t} A \left(\frac{-\cancel{2}mv_x}{\cancel{\Delta t}}\right)$ .

Let us define n = N/V as the particle density per cubic meter (total particles over volume). The force along the x direction thus simplifies to:

F_x = n A m v_x^2\label{ref5}

To relate this to the pressure on the surface of the box, we can remember that $P_x = \frac{F_x}{A}$ and so by dividing both sides of equation ( $\ref{ref5}$ ) by the area $A$ we obtain: $P_x = nmv_x^2$ . Before taking the next step, we will multiply and divide by 2 in order to make more apparent the presence of the Kinetic Energy in the equation. Our equation becomes:

P_x = 2n \left(\frac{1}{2}mv_x^2\right)

Let's recap our goal: We are trying to find a relationship between P, V and T for a gas, based on first principles arising from the motion of its particles. We have made a few assumptions:

The particle collisions are perfectly elastic
The particles obey Newton's laws

So far we have a direct relationship between the Kinetic Energy of a particle along direction-x and the Pressure along x. However we would like the pressure on all the walls, and how it relates to the average kinetic energy in all directions. We will make a new assumption

The average velocity of the particles is zero and has no preferred direction (x, y and z are equivalent).

Since there is no preferred direction, we can say that the average of the velocity squared should be equal in all directions. In other words:

< v_x^2> = <v_y^2> = <v_z^2> \label{equal_velocities_squared}

Where the brackets < $\cdot{}$ > represent the average of the magnitude inside them. In addition, the total velocity can be found from the components of the velocity by applying Pythagoras in 3D.

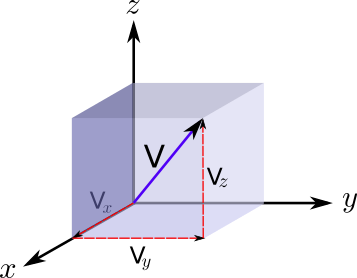
3d-velocity

Thus simply:

v^2_x + v_y^2 + v_z^2 = v^2 \label{pythagoras_velocity}

Combining equations ( $\ref{equal_velocities_squared}$ ) and ( $\ref{pythagoras_velocity}$ ) it follows that $3 <v^2_x> = v^2$ or $<v^2_x> = \frac{v^2}{3}$ . This allows us to rewrite the pressure in terms of the average velocity squared (not just in the x direction). Inserting this back into the Pressure equation, and reminding ourselves that n=N/V:

P = \frac{2}{3} \frac{N}{V} \left( \frac{1}{2} m <v^2> \right)

In other words: The total pressure of the gas in the box is inversely proportional to the volume and directly proportional to the average kinetic energy of the molecules. Let's rename the average kinetic energy as KE, so we can write:

P V = N \left[\frac{2}{3} KE \right] \label{PVKE}

We have thus almost reached our destination. The product of pressure (P) and volume (V) in a gas is equal to the number of molecules in a gas times two-thirds of the Kinetic Energy. But how is KE related to the temperature?

The final step is one that was established experimentally. The constant connecting kinetic energy and Kelvin temperature is called the Boltzmann constant k. A multitude of experiments showed that

PV = N (1.3806 \times 10^{-23}) T \label{PVBoltzmann}

Thus, if we look at equations ( $\ref{PVKE}$ ) and ( $\ref{PVBoltzmann}$ ) we can recognize that average kinetic energy and temperature are related by:

\frac{3}{2} k T = < \frac{1}{2} m v^2>

Thus we have found the equation governing the pressure, volume and temperature of an ideal gas:

PV = NkT

An alternative formulation that you will often see uses the gas constant R and the number of mols n, where nR = Nk.

Bibliography

Feynman Lectures - Lesson 39

Thanks: Special thanks to Mia Oleksak for her comments on the draft.